Free Preview
To better define conditional rules, I want to show you another way to think about them. This will deepen our understanding of the rules, and I always want you to have the most complete understanding possible of how these things work. Someone who can merely work with things mechanically is never as good as someone who really understands what they are doing, and working with conditional statements is no exception.
In the last lesson, we stated that conditional rules are rules a special kind of relationship between two things. They are connected, such that if one is true, then the other must be true as well. For example, if you drop any object on Earth, then it will eventually drop. Or, if water at one atmosphere of pressure is cooled below zero degrees Celsius, then it will freeze.
The World of Possibilities
Another way to think about conditional rules is that once stated, they limit the possibilities for how things can be in the world. When first exploring these rules and working with them, it is good to put the possibilities down on paper. Let’s do that.
Remember how in the last lesson we said that you should think of the conditions within these rules as things that could have a value of either true or false. Here is a rule:
If Evan goes golfing, then Josh goes golfing
“Evan goes golfing” is the sufficient condition. It being true is sufficient to know that Josh also goes golfing. “Josh goes golfing” goes golfing is the necessary condition. It must necessarily true in order for the sufficient condition to be true.
This rule tells us three very definite possibilities for what can happen if this rule is true (if what happens definitely will follow the rule):
Possibilities with the rule Evan goes golfing —-> Josh go golfing:
- Possibility #1: Evan goes golfing, and Josh does too (Evan goes golfing is true. Josh goes golfing is true as well)
- Possibility #2: Evan does not go golf, and Josh does too (Evan goes golfing is false. Josh goes golfing is true)
- Possibility #3: Neither goes golfing. (Evan goes golfing is false. Josh goes golfing is false)
What is not possible under the rule is that Evan goes golfing and Josh does not (Evan goes golfing is true, Josh goes golfing is false).
Not possible with the rule Evan goes golfing —-> Josh go golfing:
- Possibility #4???: Evan goes golfing, and Josh does not (Evan goes golfing is false. Josh goes golfing is false)
Until you get good at just seeing it in your head, draw all the possibilities out for any given conditional rule you encounter. We can do this with what is called a “truth table.” We will diagram the rule in condensed form Eg —-> Jg, but, remember, it is still the same rule:
Truth Table for Eg —-> Jg
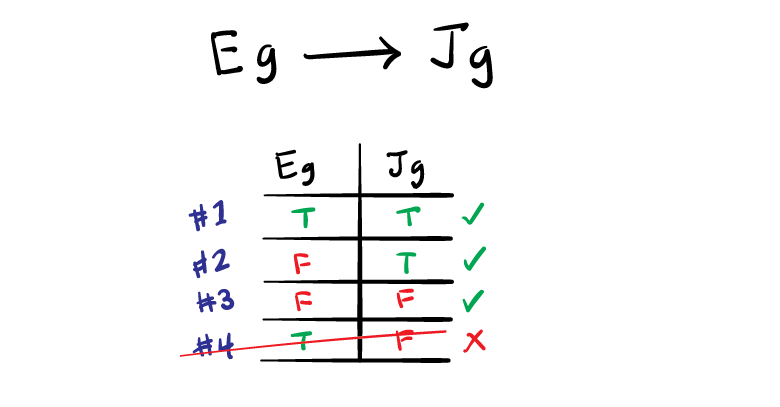
In blue, we have the four different combinations of truth values that are possible in the absence of the rule. Add the rule, and like when we wrote in all out, #4 is not possible. With the rule in place, you cannot have it be true that Evan goes golfing, and false that Josh goes golfing.
Note that saying “it is false that Josh goes golfing” is the same as saying, “Josh does not go golfing.”
Real World Truth/Falsity Doesn’t Matter
From the start, there is one important habit of my mind I want to instill while we are talking about the possible truth values of conditions in conditional statements: we are not talking about whether something is true or false in real life. For now, I want you in the habit of mind that if the LSAT tells you something is the case, you may as well take it as the word of God that it is. What you do or don’t know about the real world does not matter at all in conditional reasoning for the LSAT.
The LSAT may frequently give you rules that conflict with what you know or think you know. Here is an example:
If people are given too much free choice in elections, they will inevitably elect a dictator
Is this rule true in real life or not? I’ll bet some of you have strong feelings one way or another about it (“no, it’s certainly not inevitable” or “yes, that’s exactly what we have seen in nascent democracies” etc.).
It doesn’t matter. In deciding whether some possibility can be true under the rule, this kind of analysis is pointless. When analyzing what you can infer from the rule alongside any other information you are given (which we’ll start doing in a couple lessons), just take the rule as a given. Don’t fight with it. Let’s do the truth table for this rule:
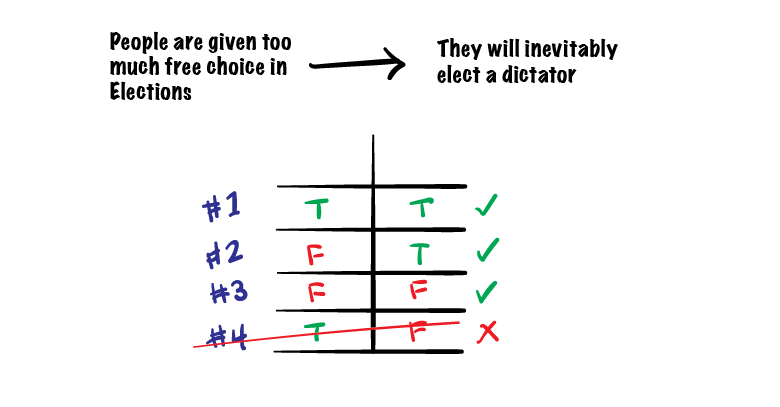
Possibilities:
#1: People are given too much free choice in elections, and they elect a dictator
#2: People are NOT given too much free choice in elections, and they elect a dictator
#3: People are NOT given too much free choice in elections, and they do not elect a dictator
Not Possible:
#1: People are given too much free choice in elections, and they DO NOT elect a dictator
So, whether you think it’s true in real life or not, it is not possible under this rule that you have a state where people are given too much free choice in elections but that does not lead to a dictatorship.
You may notice the truth table is exactly the same here as with the golfing example. The truth table always looks like that for any conditional rule following the form “if X then Y.” We’ll see different truth tables later when we add negatives.
Now that you have had your first warning (of many) not to bring your real world assumptions to the table, let’s move on. The next unit will be a test where you can make these truth tables for a bunch of conditional statements. Soon, you’ll just start seeing these possibilities in your head. If it makes it easier for you to visualize, right now, practice by making a conditional rule about some situation you understand intimately. Here’s my example:
A group of skiers is deciding whether to get on a chairlift. If Evan rides, then Justin will too. We diagram this with our arrow, like so:
Evan rides chairlift —-> Justin rides chairlift
From that rule, there are three possible arrangements for Evan and Josh on the chairlift. Let’s take a look at those.
Possibilities with the rule Evan rides chairlift —-> Justin rides chairlift:
- Evan rides with Justin
- Justin rides without Evan
- Neither Justin nor Evan ride
Not possible with the rule:
- Evan rides —-> Justin does not ride
Super easy, huh? Do this yourself with your own example just to humor me. We need to start developing a muscle in your brain that sees these combinations instantly.
Now, let’s do a quick quiz
Quiz
Review Question: For the following conditional statement, which part is the necessary condition?
If the Earth is flat, then you can fall off of the Earth’s edge
Answer Choices:
A) The Earth is flat
B) You can fall off of the Earth’s edge
Question 1: What combinations are possible with the following rule?
If Josh eats dinner, Gretchen will eat with him
Answer Choices:
A) Josh does not eat dinner, but Gretchen does
B) Josh eats dinner, but Gretchen does not eat with him
C) Josh does eat dinner, and Gretchen eats with him
D) Josh does not eat dinner, and neither does Gretchen
Question 2: What combinations are possible with the following rule?
If melons are a fruit, then they have seeds
Answer Choices:
A) Melons are not a fruit and have seeds
B) Melons are a fruit and have seeds
C) Melons are a fruit and don’t have seeds
D) Melons are not a fruit and don’t have seeds
Answers:
Review Question: B
Question 1: A, C, and D are possible. B is not
Question 2: A, B, and D are possible. C is not
